OKLAB Support?

[urzeye]

The pictures show the effect of posterisation, the second picture shows the posterisation of RGB channel, the third picture shows the posterisation of Lightness channel only, which comes from a question that I have, what is the necessary information, I have made two different ways to deal with it, one is to divide it into the same number of steps, the other is to divide it by the same luminance difference.

As you can see, if the luminance difference is small it seems pointless to divide too many levels, because the human eye doesn’t seem to see any clear difference between some of the levels. This can perhaps be applied to different areas of the picture by assuming a minimum luminance difference value perceived by the human eye, and then using this minimum value as a criterion, the parts that need to be emphasised can be assigned levels with smaller luminance difference values, while the unimportant ones can be assigned levels with larger luminance difference values.

[whirligraph]

I forgot to make something clear in my original posts.

My most-needed feature is oklab-based Normal blending mode. This would let me layer semitransparent gradients and have their color blending operate on oklab logic. This is something that would be difficult or impossible to jerry-rig - I would basically have to build a layer editor in css myself. Oklab versions of other blending modes would also be very helpful and are also currently nonexistant elsewhere from what I know. But I would be very pleased with even just oklab Normal.

My second-most-needed feature is oklab-based gradients. I am able to jerry-rig this, but it is a very time-consuming process. It would be nice to not have to transfer an armful of hex values every time I need a gradient.

To be honest my least-needed feature is a native oklab color picker. There is already multiple online oklab color pickers out there that I can just copy values from into krita. That said, I definitely think this should eventually be implemented. Having to transfer over values is still a pain. Additionally, many of these color pickers are open source and could be good reference for any devs looking into the technicalities of implementation.

If I have overlooked any functionalities please tell me! But this is about where I am at.

[Lucifer]

I support your conclusion of normal blending mode in oklab space being the top most needed feature if krita wants to have oklab support. if there is such blending mode, then gradient tool would automatically be interpolating in oklab space when going to transparent. But my understanding of krita would be that it does the blending based on your selected color space/profile.

oklab color pickers can be added to krita right now but would not actually affect how your image turns out as that depends on the color space/profile you are working in. if krita were to implement it, it would be important when selecting colors to know about the gamut limit of various standards you are outputting the image to much like the oklch website.

[Jaivu]

Would love to see it implemented, looks natural to me along with spectral mix.

[urzeye]

Hi, all, this is an experimental Oklab icc profile, hope it can help those artists who need it, here is how to use it:

This way you can use the gradient tool or normal blending mode to get the Oklab blending effect.

[Jaivu]

Many thanks, @urzeye. I’ll give it a try.

[acc4]

Thanks for making it available!
I have no idea how it works but it looked really good when I compared it in krita.

Are you developing this further? If so, do you have a github page or somewhere else that I can track your development?

[acc4]

The one problem I noticed is that it messes up the blending modes.

• Some blending modes such as Color, Luminosity are not available with this icc.
• Some blending modes behaves oddly- e.g: Multiply is always applied as neon blue, Screen is always applied as orange.

[Jaivu]

I believe he mentioned that it will only work in normal blending mode for the Oklab to work.

Here’s a quick paint.

[urzeye]

Sorry, I’d love to continue with this research, but in reality there are a lot of problems waiting to be solved.

[urzeye]

It looks like it worked, I used the latest little-cms to create the built-in Oklab profile, but krita doesn’t seem to support it at the moment because krita currently uses rawdata in memory to create the lcmsprofile, but the Oklab profile created by little-cms can’t be stored and can’t generate an icc, so I modified some code to create the profile directly when the colour space is lab, instead of using rawdata, which must be incorrect of course. But the Oklab profile created by little-cms can’t be stored and can’t generate icc, so I modified some code to create Oklab profile directly when the colour space is lab instead of using rawdata, of course this is definitely incorrect as it breaks a lot of the original functions, but at least it proves that krita can support the Oklab profile created by little-cms internally. The Oklab profile provided above has some flaws, one of them is that it doesn’t support the full floating point range, the range of L is 0~FLT_MAX, the range supported by a and b is only -0.5~FLT_MAX, ideally it should be FLT_MIN~FLT_MAX, which of course doesn’t matter for artists who only work in 8-bit or 16-bit, so I’m looking forward to krita supports the full range of Oklab profiles, and I think the ability of Oklab to handle high dynamic range colours is another big plus compared to CIElab.

[rkspsm]

I was very excited about Oklab, since the day I learnt about it. There are four areas I can think of where oklab can be useful in krita. First is of course a dedicated colorspace for a layer or entire image, but I dont see myself using it.

Secondly, as mentioned by some users above, a normal blending mode utilizing oklab. This can be immensely useful while still retaining the image in srgb colorspace (which has its advantages too).

Thirdly, in some of the filters, like curves, where we already get options like lightness and saturation in addition to the usual RGBA.

And last but not least, and an OkLCH based color picker, which as others mentioned, is merely a polar form of OkLab. However on this note, I already implemented such a color picker and has been using it for a long time now.

This color picker allows me to change color based on either keeping hue constant (left side) or the value constant (right side), hue and value being in oklch terms (hue=h, value=L). The problem is that I wrote this addon in a way which assumes lots of things available on my own system and not easily portable or installable. There were some issues like numpy python library not available for the python krita is using, so I had to manually fix it.

Other than that, its a straight up implementation of the code described by Björn Ottosson (creator of oklab and oklch) on his blog, just using python numpy code. If anybody wants I can share the relevant source for this (its part of a larger addon which I implemented with many little features), but again, I dont know how hard/easy it will be to use on your krita installation on your platform/machine.

[urzeye]

I think changing the color space configuration file for 16 bit and 32 bit floating-point CIElab to Oklab seems to be a good choice, because CIElab only supports the lightness range of floating-point 0~1.0, while Oklab’s profile does not have good support for 8-bit integers and 16-bit integers because unit8 and unit16 do not have negative numbers and cannot support a and b well.

[rkspsm]

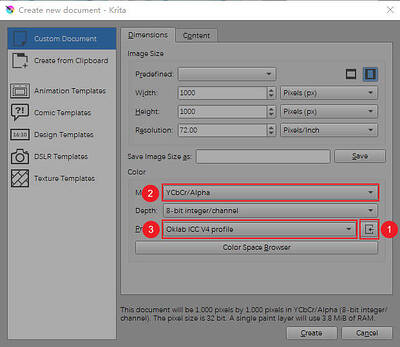
Oklab’s profile does not have good support for 8-bit integers and 16-bit integers because unit8 and unit16 do not have negative numbers and cannot support a and b well

From what I know from my own attempts at playing with colors, the problem is not really about negative numbers, its about memory constraints. I mean if you only need 128 negative numbers, then you can emulate it with uint8, there will be just one extra step in many operations.

Also, anything above 8-bit starts to become problematic with huge images with several layers, unless you have a very beefy machine. This is one major reason why I prefer to stay with 8 bit mode.

Then there are several blend modes which are available only if you are working with rgb/srgb, and they can often prove quite useful in many situations. Combine this with the above, I’d personally prefer to work with 8-bit srgb images when doing painting. I cannot say about photography retouching workflows as I dont have much experience with that, but I have heard that they have their own set of complications and oklab may not be a very good choice for that.

This is why, atleast as per my workflow, blend modes solve all those problems. An oklab-normal blend mode can be used for most tasks. And additional blend modes like oklab-color or oklab-value may also be useful if used with brushes.

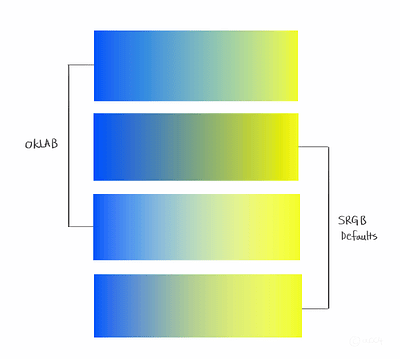
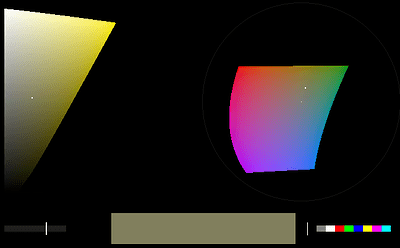
The color picker which I wrote for myself using oklch doesnt allow picking values which give invalid rgb result. But because 8-bit is constrained with memory, there are some “holes” in the colorspace, especially in the deep blue region.

So far I have not found that anomaly for some other color, only in that very narrow region of pure blue hue.

The point is, this is one problem that can be easily solved by using 16-bit or 32-bit floating point, but then again, even if your machine does have memory and cpu to handle that or if you dont usually work with large images/layers, most monitors work in srgb colorspace only, so they still wont be able to display the color which oklab is pointing to when its value is falling inside those gaps. Or atleast thats what my understanding is, I might be wrong.

[urzeye]

Yes, it is true that we can get oklab to work at 8-bit by some means, such as offsetting the ab value by 0.5 as in the oklab icc profile I provided above, but the reason I prefer to use oklab in 16-bit or 32-bit floats is because they can either retain the colour information beyond the 8-bit srgb, and then use gamut clipping to maintain the luminance, or use the tonemap etc, whereas using it in 8-bit is likely to result in hard clipping beyond the gamut, and is irreversible.

[urzeye]

Honestly I like the float point mode because I don’t have to think too much about it, I just need to know how the real light works, it makes it a bit easier for me, thanks krita for having the float point mode, krita is the best in my mind.

[rkspsm]

Yes you are right, hdr image processing is bad with 8 bit, there is just not enough bits to store the information. I was talking mainly from drawing/painting point of view, the typical workflow which includes some kind of line drawing, and then you block it with colors and then refine it with blend modes, filters and a lot of brush work. That is what I spend most of my time doing, and I have tried using higher bit modes for that but it didnt give me any benefit.

The thing with oklab is, that I have heard mixed claims of its success with hdr images when compared to some other models. Just googling “oklab hdr” gives lots of info on that. Not saying I understand all of it, but I am just pointing out that while I understand what HDR is (large memory for each color channel, to store huge range of colors), I have limited knowledge of algorithms and colorspaces used for that purpose, eg there is JzAzBz, and then there is filmic RGB. I have read a little about them but that was only in relation with standard rgb (or why they are superior to standard rgb).

Also there are softwares like darktable which is dedicated to hdr photo manipulation. Only after playing with it a little bit I realized that whatever photo manipulation I ever did in Krita is probably very basic compared to whatever requirements these kinds of softwares are designed for. Again, not my expertise and I tend to have very large images when doing painting in Krita and about 7-8 layers on average, which is not that many. If I use 16-bit or more, even the simplest filter operations take like forever.

Lastly, and it might have changed/fixed now, there are some blend modes which I use, which dont work in anything but 8 bit integer rgb, and if used with anything else they produce huge mess or outright crash, but I havent tested that recently.

[urzeye]

Yes, hopefully all these problems can be solved, honestly I feel your colour picker is great, if I had more time I might consider porting it to krita if you’re willing to open source it, but I’ve got a lot of things I need to do lately so I don’t have more energy to think about it all, thanks for your reply, I’ve learned a lot of unknowns .

[rkspsm]

I also wrote a toy paint program with oklab as the one and only blend mode just to try out how it actually feels if I paint with an oklab based brush. I chose a reference image, a photograph of some park in fall/winter setting, it had lots of colors in it.

And I cannot even begin to describe how amazing it was !! The way colors blended together, for any combination. The image had all the usual elements of a natural landcape, sky, clouds, hills, trees, flowers, mud, dirt, gravel. With usual brush in normal rgb mode, its constant struggle to keep correcting color because they dont mix the way I imagine them mixing in my head.

With oklab I expected it to be somewhat easier but it was much much more than that. It was not just easy, it was trivial and effortless and a heck lot more fun ! The image was represented as uint8 array in memory, but the actual blending logic was performed with 32-bit floating point and then converted back to uint8.

I only wish it was possible to implement custom blend modes in krita by plugin API, but afaik its not, atleast not yet.

[Lucifer]

sounds awesome!! i also use krita primarily to paint and use alot of layers in my file. having the layers stored as what the user sets as their depth but blending operations at higher depths is how i imagined oklab as a blending mode needs to be.